diumenge, 6 de desembre del 2009
CURIOSITAT MATEMÀTICA DE LA LAIA I LA LÍDIA
-1r: demana-li a un amic que a l'edat que té li sumi 90.
-2n: al resultat d'aquesta suma, ha d'eliminar el nombre que ocupa el lloc de les centenes i sumar-lo al número que ha obtingut.
-3r: ara li preguntes la quantitat i li sumes 9.
Seguint aquestes operacions podràs saber l'edat de qualsevol persona major de 10 anys.
EXEMPLE:
Edat: 50 anys
50+90=140
(1)40+1=40+1=41
41+9=50 (aquesta operació només la realitza l'endevinador).
dimecres, 2 de desembre del 2009
Oriol Casas i Àlex Espinal: El número 2

Hola som l'Oriol Casas i l'Àlex Espinal i us volem presentar un joc matemàtic molt curiós que hem trobat, diu el següent:
Un dia vaig recordar un vell joc mirant un programa a la televisió que consisteix en formar tots els números del 0 al 10 utilitzant només cinc cops el nombre 2 i el signes + , - , x i : . Respectant l'ordre de les operacions (primer multiplicacions i divisiones en l'ordre en que apareixen i després sumes i restes)
Així es pot formar:
0 = 2 – 2/2 – 2/2 = 2 - 1- 1 = 1 -1= 0
1 = 2 + 2 – 2 – 2/2 = 2 + 2 - 2 - 1= 4 - 3 = 1
2 = 2 + 2 + 2 – 2 – 2= 6 - 4= 2
3 = 2 + 2 – 2 + 2/2 = 4 - 2 + 1= 2 + 1= 3
4 = 2/2 + 2 + 2/2 = 1 + 2+ 1= 4
5 = 2 + 2 + 2 – 2/2 =6 - 1= 5
6 = 2 + 2 + 2 + 2 – 2 = 8 - 2 = 6
7 = 2 × 2 + 2 + 2/2 = 4 +2 + 1= 7
8 = 2 × 2 × 2 + 2 – 2 = 8 + 2 - 2 = 8
9 = 2 × 2 × 2 + 2/2 = 8 + 1= 9
10 = 2 + 2 + 2 + 2 + 2 = 6 + 4 = 10
Però el més entretingut és que cada resultat d'aquest joc no és únic. Per exemple, per construir el número 4 podem fer : 4 = 2/2 + 2 + 2/2 però una altra manera és : 4 =2 x 2 x 2 -2 -2 .
Andreu Oròs i Guillem Allepuz: El nombre Phi
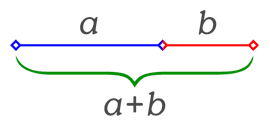 El nombre Phi és la relació entre un segment /a/ i un segment /b/ de tal manera que el valor d'a/b sigui 1,618033...
El nombre Phi és la relació entre un segment /a/ i un segment /b/ de tal manera que el valor d'a/b sigui 1,618033...La proporció àuria podríem dir que és aquella proporció que es fa agradable i/o harmoniosa a la vista.
Posem l'exemple del DNI per a entendre-ho millor:

Àfrica i Alba
dimarts, 1 de desembre del 2009
Júlia Anguera i Berta Junyent
La nostra curiositat matemàtica tracta sobre endivinar el número que pensa l'altra persona realitzant sumes i restes mentals.
Us ho explicarem mitjançant un diàleg:
-Jo: Pensa't un número.
-Participant: (5)
**(El que ve ara us ho podeu inventar):
-Suma-li 3, s'uma-li 5 i suma-li 2.
**(El participant li sumarà a 5 3+5+2=10, li donarà 15)
**(Jo únicament sumaré 3+5+2=10)
-Jo: Resta-li el nombre que t'has pensat al principi.
**(El participant realitzarà: 15-5=10
-Jo: És 10.
-Participant: Molt bé.
Us recordem que sabem el que li dóna la operació al participant perquè simplement sumem el que li hem dit nosaltres, perquè al restar-li el número que shavia pensat ell, només ens queden els nombres que li hem manat que sumés.
Som el Marcel i l'Anton, alumnes de 2n ESO, i em trobat una curiositat matemàtica relacionada amb el nombre 1
1·1= 1
11·11= 121
111·111= 12321
1111·1111= 1234321
11111·11111= 123454321
111111·111111= 12345654321
1111111·1111111= 1234567654321
11111111·11111111= 123456787654321
111111111·111111111= 12345678987654321
El nombre d'1 multiplicat per l'altre nombre et dona la quantitat d'1 en nombres del 1 al 9 per exemple:
11= 2 xifres, per tan, 11·11= 121 --- 2 xifres
Contem fins, en aquest cas, 2(12_) i tornem enrere fins l'1(121)
Desxifra el nombre

Aquesta curiositat consisteix en desxifrar quin nombre ha pensat la persona ,amb la qual estàs jugant, a través d’operacions matemàtiques bàsicament de càlcul mental.
Primer de tot: per poder realitzar aquesta curiositat hem de tenir sis taules amb uns nombre determinats que són els següents:
1 3 5 7 9 11 13 15 17
19 21 23 25 27 29 31 33 35
37 39 41 43 45 47 49 51 53
55 57 59 61 63
16 17 18 19 20 21 22 23 24
25 26 27 28 29 30 31 48 49
50 51 52 53 54 55 56 57 58
59 60 61 62 63
32 33 34 35 36 37 38 39 40
41 42 43 44 45 46 47 48 49
50 51 52 53 54 55 56 57 58
59 60 61 62 63
8 9 10 11 12 13 14 15 24
25 26 27 28 29 30 31 41 42
43 44 45 46 47 40 56 57 58
59 60 61 62 63
2 3 6 7 10 11 14 15 18
19 22 23 26 27 30 31 34 35
38 39 42 43 46 47 50 51 54
55 58 59 62 63
4 5 6 7 12 13 14 15 20
21 22 23 28 29 30 31 36 37
38 39 44 45 46 47 52 53 54
55 60 61 62 63
Després el jugador es pensa un número entre 1 i 63. Tot seguit va observant les taules i mira si el seu nombre hi apareix; si és així diu: "sí que hi apareix" i si és que no diu el contrari.Aixó s'ha de fer amb totes les sis graelles. Nosaltres ens hi hem de fixar molt bé perquè quan ens diu que sí hem de sumar els nombres que aparèixen en primera posició ja que tots aquests sumats donen 63.
Per aquesta raó endivinarem el nombre que el nostre jugador ha pensat.
Exemple: ( hem penso el número 23)
--> en la primera graella si que surt
--> en la segona graella si que surt
--> en la tercera graella no surt
--> en la quarta graella no surt
--> en la cinquena graella si que surt
--> en la sisena graella si que surt
Ens hem de quedar amb els nombres: 1, 16, 2 i 4 perquè són els primers nombres de la graella i en aquestes el nostre nombre si que surt. I ara sumem: 1 + 16 + 2 + 4=23! El nombre que haviem pensat.
diumenge, 22 de novembre del 2009
EL NOMBRE 9
Hola! Som la
A tothom ens costa multiplicar pel nombre 9 perquè és un nombre gran, etc. Doncs us ensenyarem una manera fàcil, ràpida i divertida per multiplicar aquest nombre.
Consisteix en:
Per començar, hem de posar els primers nombres, col·locant-los de menor a major.

9·2 =
9·3 = 2
9·4 = 3
9·5 = 4
9·6 = 5
9·7 = 6
9·8 = 7
9·9 = 8
9·10 = 9
| Hem de col·locar els segons nombres, de major a menor |
9·1 = 09
9·2 = 18
9·3 = 27
9·4 = 36
9·5 = 45
9·6 = 54
9·7 = 63
9·8 = 72
9·9 = 81
9·10 = 90
dijous, 19 de novembre del 2009
El nombre màgic!
Es tracta d'un nombre clínic. Els nombres clínics es formen al dividir 1 entre qualsevol altre nombre. En el nostre cas dividim 1 entre 7 i el resultat és: 0,142857142857....
El nombre 142857 no és un nombre normal i corrent sinó que és tot el contrari. Ara ho expliquem.
Si multipliquem 142857 per qualsevol nombre del 1-6 ens donarà el mateix nombre però amb les xifres barrejades.
142857*1=14285

142857*2=428571
142857*3=285714
142857*4=857142
142857*5=571428
142857*6=714285
En canvi el 142857*7=999999
I aquí no s'acaba tot.
14+28+57=99
142+857=999
Quan multipliquem el nombre màgic per nombres superiors a 7 per aconseguir 142857 hem de sumar algunes xifres:
142857*8=1142856; si sumem 1+6= 7; per tant això dona 142857
142857*9=1285713
142857*10=1428570
142857*11=1571427
Si dividim qualsevol nombre inferior a 7 el resultat donarà:
3/7= 0,428571
4/7= 0,285714
5/7= o,857142
6/7= 0,571428
I per acabar...:
142 al quadrat= 20164
857 al quadrat=734449
Si restem 734449-20164 Endevineu el resultat?
dimecres, 18 de novembre del 2009
Endevinar el pensament

En Carlos i en Marc presentem un joc matemàtic amb el qual podem endevinar el que pensa una altra persona.
Primer, la persona a la que se li fa el truc ha de pensar un número entre el dos i el deu. A continuació ha de multiplicar el número per nou i suma les seves xifres ( per exemple 12, 1+2=3). Després ha de restar 5 al número que té. A continuació ha de passar aquest número a lletres, és a dir, 1 és igual a A, 2 és igual a B, 3 és igual a C, 4 és igual a D…Una vegada té la lletra ha de pensar el nom d’un país que comenci per aquesta lletra. Després ha de pensar el nom d’un animal en castellà que comenci per la segona lletra del país escollit. Finalment, la persona que fa el truc diu: “A Dinamàrca no hi ha iguanes”. Si el truc ha sortit bé, la persona a la que se li fa el truc ha d’haver pensat justament Dinamarca i iguana.
Això es deu a que sempre que multipliquem un número entre el 2 i el 10 per 9 i sumem les seves xifres el resultat sempre és 9.
2x9=18 1+8=9
3x9=27 2+7=9
4x9=36 3+6=9
5x9=45 4+5=9
6x9=54 5+4=9
7x9=63 6+3=9
8x9=72 7+2=9
9x9=81 8+1=9
10x9=90 9+0=9
Com a conseqüència sempre que li restem 5 a 9 donarà 4, i la lletra serà la D. El primer país que sen’s acudeix és Dinamarca, i la primera lletra de l’animal és la I i el primer animal que sen’s acudeix comenci és l’ iguana. D’aquesta forma, si la persona a la que se li fa el truc calcula bé, és molt difícil equivocar-se.
dilluns, 12 d’octubre del 2009
Escacs i matemàtiques
 Els escacs, una activitat ben nostra, tenen una curiosa i coneguda relació amb les matemàtiques. Si obres la web següent descobriràs això i moltes coses més...
Els escacs, una activitat ben nostra, tenen una curiosa i coneguda relació amb les matemàtiques. Si obres la web següent descobriràs això i moltes coses més...
Jordi Carmona
http://www.redescolar.ilce.edu.mx/redescolar/act_permanentes/mate/nombres/mate1k.htm
Galeria d’escacs:
http://www.chess-poster.com/spanish/galeria/galeria.htm
Benvinguda
Cal que cada trimestre facis al menys una entrada d’una curiositat matemàtica que hauràs d’explicar a classe.
Les entrades no han de tenir cap falta d’ortografia.
Es valorarà per l’avaluació de la teva aportació:
1. L’interès de la notícia, ressenya, curiositat, etc.
2. La qualitat de la redacció.
3. L’adequació del nivell de dificultat als coneixements que tenim a 2n d’ESO.
4. La capacitat i claredat de la teva exposició a classe.
5. La vinculació a altres pàgines i links.
6. La relació amb els temes que estem fent aquest any a matemàtiques.
7. Els links que aportis amb vídeos, pàgines interactives, imatges, etc.
8. Totes les entrades han d’anar signades amb el teu nom i cognom i la identificació de la teva classe.
Jordi Carmona
Professor
