ELS DAUS MÀGICS

Hola som l'Àlex Espinal i el Carlos Garcia i hos exposem el seguent enigma:

Aquest és un petit joc o truc en el que es pot demostrar que ets capaç de sumar les cares ocultes d'una torre de tres daus. Hauràs de demanarl-li a una de les persones que t'observin que apili els daus sense que la vegis, i un cop acabat que t'avisi.

Hauràs de restar-li a 21 al número del dau de dalt de tot de la torre i aquest serà la suma de les cares ocultes. També pots demanar a la gent que t'ho posi més difícil apilant cuantre daus,y llavors, per endivinar la suma de les cares ocultes s'haurà de restar a 28 el número del dau del cim de la torre.

Aquest truc es basa en què les cares oposades d'un dau de sis cares sumen 7.

Igualtat de 72

Hola, som la Clàudia i la Joana i la nostre curiositat va sobre una igualtat de 72.
És curiós que de vegades, veus com una sèrie de números que en principi no tenen cap relació de cap tipus, pots acabar-los trobant una lògica:
2 + 5 + 13 + 16 + 17 + 19 = 3 + 6 + 12 + 16 + 17 + 18
Evidentment, aquesta igualtat és certa, 72 = 72. Però, què passa si ho elevem tot al quadrat?
4+25+169+256+289+361 = 9+36+144+256+289+324 ??

1104 = 1058
Com veieu, encara que als dos costats la suma sigui 72, al elevar els valors al quadrat no obtenim una igualtat.
No hem pogut descobrir perquè passa això però continuarem investigant-ho per poder explicar-ho.

EL TRIANGLE DE TARTAGLIA

Som la Marta i l'Àfrica i presentem la nostra curiositat matemàtica, El Triangle de Tartaglia.

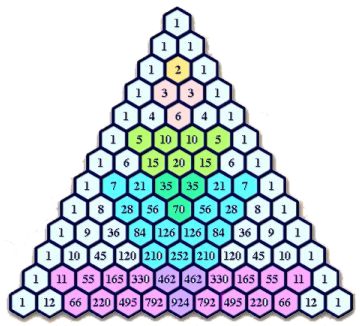
Aquest triangle es genera a partir de situar el número 1 al seu extrem superior, a partir d’aquí les successives files es construeixen col·locant un 1 a cada cantonada i la resta de caselles és igual a la suma dels dos nombres que té al damunt en una infinita sèrie d’uns laterals i de sumatoris de caselles que produeixen un incessant augment dels nombres que el composen.
Doncs bé, aquesta figura, que podria semblar pels neòfits un simple entreteniment de càlcul, amaga una diversitat de propietats i curiositats tan gran que el converteixen en un petit univers matemàtic en sí mateix i una eina d’immensa utilitat en el camp numèric, etc.
Els matemàtics de totes les èpoques, des del seu descobriment, han posat els seus ulls en ell i han buscat tota mena de sorprenents relacions, utilitats i recursos.

Aquestes són algunes de les seves característiques:

- El número 1 de l’extrem superior del triangle es considera com la fila zero.

- Cada número es genera a partir de la suma dels dos nombres que té a sobre.
Així, per exemple, els dos uns de la fila 1 sumats formen el 2 central de la segona fila.
La tercera fila es forma a partir del 1 + 2 = 3 i 2 + 1 = 3. La quarta és 1 + 3 = 4, 3 + 3 = 6, etc.

- Totes les files mostren una estructura simètrica, les de ordre parell tenen un número central únic, les de ordre senar tenen dos nombres idèntics al centre. La suma de cada semifila imparell és, òbviament, igual.

- La suma dels nombres de cada fila és igual a 2 elevat al número de la fila.
La quarta fila, per exemple: 1 + 4 + 6 + 4 + 1 = 16 = 2⁴. La sisena 1 + 6 + 15 + 20 + 15 + 6 + 1 = 64 = 2⁶

- Cada fila expressa les successives potències del número 11, les quatre primeres de forma clara, i a partir de la cinquena fila, si una casella està formada per més d'una xifra, hem de fer una senzilla suma portant-se alguna xifra. Exemple:

11⁰ = 1, 11¹ = 11, 11² = 121, 11³ = 1.331, 11⁴ = 14.641 Ara comencen els canvis: 11⁵seria 15(10)(10)51, però fem la suma portant i obtenim: 11⁵ = 161.05111⁶ = 16(15)(20)(15)61 => 11⁶ = 1.771.561, etc.
I així fins moltes més.

L'ÀVIA PRESUMIDA

"- Quants anys tens? - pregunta a la Maria una amiga.
- Tants com indiquen les dues darreres xifres de l’any del meu naixement - respon la Maria.
- El mateix dic - diu l’àvia de la Maria, que està fent mitja en un racó, però que no perd detall de la conversa.
- Àvia! - exclama la Maria -, està bé que et treguis uns quants anys, però no pretendràs tenir la mateixa edat que jo.
- Doncs en aquesta ocasió no m’he tret cap any...- protesta l’àvia, i s’ho demostra ensenyant el seu DNI.
Quina és l’edat de la Maria i de la seva àvia si la conversa va esdevenir dos anys després de les Olimpíades de Barcelona ’92?"

• L'edat de la Maria:

1994-(x+1900)=x

2x=1994-1900

x=94/2=47

Posem 1994 perquè és l'any de què parlem, i li restem l'edat de la Maria més 1900, que sumen l'any en que va néixer. Això ens donarà l'edat de la Maria.

• L'edat de l'àvia

1994-(y+1800)=y

2y=1994-1800

y=194/2=97

Posem 1994 igual que abans, li restem l'edat de l'àvia més 1800, perquè no pot ser la mateixa que la Maria. Llavors obtenim l'edat de l'àvia.

En aquest punt podem comprovar si el que hem averiguat coincideix amb l'enunciat:

• 47+1947=1994

• 97+1897=1994

La "X"

Som l'Àfrica i l'Alba i hem triat aquesta curiositat perquè tracta de la X.

Quan utilitzem la x, que és una lletra molt comuna en les equacions hem d'anar amb compte de no confondre-la amb l'abecedari:

Sabeu què dóna aquesta expressió?

(x-a)(x-b)(x-c)(x-d)...

Doncs dóna 0. Per què? Perquè si seguim fent-ho fins al final...

(x-a)(x-b)(x-c)(x-d)(x-e)(x-f)(x-g)(x-h)(x-i)(x-j)(x-k)(x-l)(x-m)(x-n)(x-o)(x-p)(x-q)(x-r)(x-s)(x-t)(x-u)(x-v)(x-w)(x-x)(x-y)(x-z)

...ens trobem que enmig de l'expressió algèbrica hi ha (x-x), que és 0 i per molts nombres o lletres multiplicant-se entre si que hi pugui haver, si es multiplica per 0, el seu resultat sempre serà 0.

Hola som l'Àlex i la Joana i us exposem aquesta curiositat matemàtica, esperem que hos agradi.
El més gran dels números de tres xifres, el 999, és sens dubte extraordinari .
Una propietat interessant d’aquest número la trobem en la seva multiplicació per qualsevol altre número de tres xifres; obtenint un producte de sis xifres: les seves tres primeres xifres constitueixen el número multiplicat, disminuït amb una unitat, i les tres xifres restants són el ‘complement’ al 9, de les primeres.
Per exemple: 573 x 999 = 572 427
Tan sols ens cal donar una ullada a la següent línia per entendre l’origen d’aquesta particularitat i començar a obrir la nostra ment a les matemàtiques:
573 x 999 = 573 x (1000-1) = 573 000 – 573 = 572 427
Coneixent aquesta particularitat podem multiplicar ‘instantàniament’ qualsevol número de tres xifres per 999:
917 x 999 = 916 083,
509 x 999 = 508 491,
981 x 999 = 980 019.

ENDEVINAR L'EDAT

Endevina l'edat

Pots endevinar l'edat d'una persona i el mes en què va néixer si fas que pensi en el nombre del mes de naixement (gener = 1, febrer = 2, ...) i després li demanes que el multipliqui mentalment per 2 i li sumi 5 al resultat. Després de multiplicar el resultat que ha obtingut per 50 i sumar la seva edat. Fes que et digui el resultat final de tots aquests càlculs i, mentalment, restal 250. El nombre obtingut tindrà 3 o 4 xifres. Les dues xifres de la dreta són les de l'edat, i les de l'esquerra són el número del mes de naixement. Sabries dir per què és així?.


Anomenem A al número del mes de naixement i B a l'edat. Seguim les següents operacions:

2A+5 --> (2A+5).50 --> (2A+5).50+B --> (2A+5).50+B-250" ">2A -> 2A +5 -> (2A +5) .50 -> (2A +5) .50 + B -> (2A +5) .50 + B-250

Operant queda: 100A +250 + B-250 = 100A + B

Així, sempre tindrem B a les unitats i desenes, i A en centenes i unitats de miler (si és el cas).